今年的基金亏的撕心裂肺,前几年两只基金小赚3万多,今年都在跌跌跌,这是今年年初购买的一只,几个月亏了一千多,我想取消定投,把基金赎回了,一个孩子上高中,一个孩子上大学了,感觉有点吃力,大家觉得基金投资还有前景吗?有没有好点基金介绍一下。
2、在格式菜单下,选wcs-显示;或者按键盘上的w键,把工作坐标显示出来。
3、选择格式,选wcs,然后在选动态,或者直接鼠标点中坐标双击,就会出现如图状态的坐标。
4、把鼠标放在任意一轴的箭头上时,就是出现两个箭头,此时双击,就可以改变坐标轴的方向。
5,把鼠标放在如图圆圈位置,就可以对坐标旋转操作。
6,把鼠标放在如图圆圈位置,就可以对坐标移动操作。
UG的坐标系是一切模型的基础,没有坐标,模型无法进行数据建模,绝对坐标在没有删除的情况下会一直存在,如果不小心删除,倒退一步,因为绝对坐标系是无法第二次进行建立的,除非把模型移到另一个新建页面打开。
双击坐标系可以修改坐标方向角度距离。
绝对坐标系:位置与方向始终不变,可以让其显示,也可以让其关闭,但无论其是否显示还是关闭,它的作用一直在起作用,其最大的作用在于决定XYZ轴的绝对方向和绝对零点,从而判断俯视图,仰视图,左视图,右视图,前视图,后视图提供依据。
工作坐标系:又称相对坐标系,它的位置和方向可以随意更改,它的作用在于所构建的二维曲线图是建立在哪个三维空间面上,UG默认的二维曲线是构建在所属工作坐标系XY平面上的。
加工坐标系:进入加工模块后用来编刀路算程序的一种坐标系,它的作用是编刀路算程序的零点,程序中所算出来的XYZ等坐标值都是以它为零点的。
总结:在同一个UG图形文件中,以上三个坐标系可以各在不同的点位上,方向也可以不一样,但让三个坐标重合是最好的,这样人为的看错数据出错的几率会大大降低,尤其是用UG编刀路算程序更应该如此。
球坐标变换里面x=rsinφcosθ,y=rsinφsinθ,z=rcosφ,里面r指的是曲面上的点到原点的距离,不是解析几何里面的半径。
解:原式=∫<0,2π>dθ∫<0,π>sinφdφ∫<0,1>[(rsinθcosφ)^2
+(rsinθsinφ)^2+(1+rcosφ)^2]r^2dr
(作变换:x=rsinθcosφ,y=rsinθsinφ,z=1+rcosφ)
=∫<0,2π>dθ∫<0,π>sinφdφ∫<0,1>(r^4+2r^3cosφ+r^2)dr
=2π∫<0,π>(8/15+cosφ/2)sinφdφ
=2π(16/15)
=32π/15。
积分区域是整个球体或者半个球体或由圆锥面与球面围成,可考虑球面坐标系;积分区域的边界是球面、圆锥面、圆柱面、旋转抛物面等,可考考虑柱面坐标系;肌敞冠缎攉等圭劝氦滑其余情况考虑直角坐标系。 上面是一般情况,有时候考虑到被积函数,坐标系的选择还会有变化,比如积分区域由平面z=1与旋转抛物面z=x^2+y^2围成,可用柱面坐标系,但如果被积函数f(x,y,z)=z,那么选择先xy后z的直角坐标的积分次序会让解题过程简单。
一:ug如何选择坐标系
1、打开ug,界面上没有工作坐标,说明工作坐标此时是属于隐藏的状态。2、在格式菜单下,选wcs-显示;或者按键盘上的w键,把工作坐标显示出来。
3、选择格式,选wcs,然后在选动态,或者直接鼠标点中坐标双击,就会出现如图状态的坐标。
4、把鼠标放在任意一轴的箭头上时,就是出现两个箭头,此时双击,就可以改变坐标轴的方向。
5,把鼠标放在如图圆圈位置,就可以对坐标旋转操作。
6,把鼠标放在如图圆圈位置,就可以对坐标移动操作。
UG的坐标系是一切模型的基础,没有坐标,模型无法进行数据建模,绝对坐标在没有删除的情况下会一直存在,如果不小心删除,倒退一步,因为绝对坐标系是无法第二次进行建立的,除非把模型移到另一个新建页面打开。
双击坐标系可以修改坐标方向角度距离。
绝对坐标系:位置与方向始终不变,可以让其显示,也可以让其关闭,但无论其是否显示还是关闭,它的作用一直在起作用,其最大的作用在于决定XYZ轴的绝对方向和绝对零点,从而判断俯视图,仰视图,左视图,右视图,前视图,后视图提供依据。
工作坐标系:又称相对坐标系,它的位置和方向可以随意更改,它的作用在于所构建的二维曲线图是建立在哪个三维空间面上,UG默认的二维曲线是构建在所属工作坐标系XY平面上的。
加工坐标系:进入加工模块后用来编刀路算程序的一种坐标系,它的作用是编刀路算程序的零点,程序中所算出来的XYZ等坐标值都是以它为零点的。
总结:在同一个UG图形文件中,以上三个坐标系可以各在不同的点位上,方向也可以不一样,但让三个坐标重合是最好的,这样人为的看错数据出错的几率会大大降低,尤其是用UG编刀路算程序更应该如此。
二:如何选择工程坐标系
1-坐标系:工程控制网一般采用国家统一的3°带高斯平面直角坐标系. 2-任意带的独立高斯平面直角坐标系:当不能满足工程对高斯投影长度变形的要求(通常不大于2.5cm/km)时,可自定义中央子午线和投影基准面,建立任意带的独立高斯平面直角坐标系,但应与国家坐标系衔接,建立双向的坐标转换关系. 3-根据工程需要,也可假定参考基准,建立假定平面直角坐标系.三:重积分如何选择坐标系
cosφ是直径1乘cosφ,就是球面上的点到原点的距离。所以r的范围是0到cosφ。参考学球坐标系下的三重积分时r范围是0到半径。球坐标变换里面x=rsinφcosθ,y=rsinφsinθ,z=rcosφ,里面r指的是曲面上的点到原点的距离,不是解析几何里面的半径。
解:原式=∫<0,2π>dθ∫<0,π>sinφdφ∫<0,1>[(rsinθcosφ)^2
+(rsinθsinφ)^2+(1+rcosφ)^2]r^2dr
(作变换:x=rsinθcosφ,y=rsinθsinφ,z=1+rcosφ)
=∫<0,2π>dθ∫<0,π>sinφdφ∫<0,1>(r^4+2r^3cosφ+r^2)dr
=2π∫<0,π>(8/15+cosφ/2)sinφdφ
=2π(16/15)
=32π/15。
积分区域是整个球体或者半个球体或由圆锥面与球面围成,可考虑球面坐标系;积分区域的边界是球面、圆锥面、圆柱面、旋转抛物面等,可考考虑柱面坐标系;肌敞冠缎攉等圭劝氦滑其余情况考虑直角坐标系。 上面是一般情况,有时候考虑到被积函数,坐标系的选择还会有变化,比如积分区域由平面z=1与旋转抛物面z=x^2+y^2围成,可用柱面坐标系,但如果被积函数f(x,y,z)=z,那么选择先xy后z的直角坐标的积分次序会让解题过程简单。
四:三重积分如何选择坐标系
12.4 直角坐标系下的三重积分三重积分假设 F(x,y,z) 为一个空间有界闭区域 D 上的函数. D 为下面立体椭球所占区域. 将空间区域分割成小长方块. 体积记为 ΔVk, 其长宽高分别为Δxk, Δyk, Δzk , 并有下列的求和式:
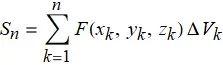
观察下面动画, 当空间不断分割, 每个小方块的体积 ΔVk 不断变小:
如果 F 连续, 且 D 的边界曲面分片光滑, 其交为连续曲线, 那么当 Δxk, Δyk, Δzk 趋近于 0 时, Sn 有极限:
空间区域的体积
如果 F 是常数函数 1 , 那么 D 的体积就是三重积分:
确定积分限先来观察下面的三重积分的直观展示动画:
如何找出三重积分的积分限, 如果先对 z 作积分, 再对 y, 最后对 x, 采用下列步骤:
第一: 画出空间区域 D 及其投影区域 R.
第二: 确定 z 积分限. 过 R 内一点 (x,y) 做一条垂直于 z 轴的直线. 在 f1(x,y) 进入区域 D, 在 f2(x,y) 离开 D. 这便是 z 的积分限.
第三: 确定 y 的积分限过点 (x,y) 做平行 y 轴的直线, 在 g1(x) 进入 R, 在 g2(x) 处离开 R, 这就是 y 的积分限.
第四: 确定 y 的积分限. x 的积分限为保罗所有通过 R 且平行 y 轴的直线.
空间 - 函数的积分平均值
F(x,y,z) 是空间区域 D 上一立体的密度, 则 F 平均值就相当该立体的平均密度, 可以有下面公式定义:
喜欢 [遇见数学] 图解系列的朋友们还请点赞, 转发! 我们会继续努力前行, 奉献更多图解数学作品.

